Die Programmiersprache R wurde bereits anfangs der 90er Jahre entwickelt. An Bedeutung gewonnen hat sie aber erst in den letzten zehn Jahren. Dies liegt zum einen am grossen Funktionsumfang und zum anderen an der Tatsache, dass Anwender nicht zwangsläufig umfangreiche Programmierkenntnisse haben müssen, um Advanced Analytics mit R erstellen zu können.
In meinem letzten Blogbeitrag „Erste Schritte mit R“ haben wir uns umfassend mit den Grundlagen befasst. Sollten Sie den Artikel noch nicht gelesen haben, dann wäre jetzt ein guter Zeitpunkt – zum Beitrag gelangen Sie hier.
Denn heute werden wir tiefer in die Thematik eintauchen und uns mit Advanced Analytics mit R befassen, im Speziellen mit der graphischen Darstellung, der Regessionsanalyse und der Zeitreihenanalyse mit R.
Lassen Sie uns beginnen.
Graphische Darstellung in R
Beginnen wir mit den Grundlagen und sehen wir uns die verschiedenen Diagrammarten an, die wir in R erstellen können. Obwohl das Erstellen von Diagrammen eine relativ einfache Aufgabe ist und man meinen könnte, dass es nicht zu den fortgeschrittenen Analysen gehört, ist es wichtig, die verschiedenen Diagrammarten zu kennen und zu wissen, wann und für welches Szenario sie verwendet werden sollten. Die Ergebnisse, die Sie so aus ein paar Codezeilen erzielen können, sind oft aussagekräftiger als so manch ausgeklügeltes Advanced Analytics.
ggplot2 – Your best Friend!
Unabhängig davon, welche Art von Diagrammen Sie in R erstellen möchten, ggplot2 sollte immer Ihre erste Wahl sein. Wenn es darum geht etwas darzustellen, dann ist es mit Abstand das von R-Programmierern am häufigsten verwendete Paket.
Schauen wir uns die verschiedenen Diagramme, die das ggplot2-Paket bietet, genauer an und finden heraus, für welche Anwendungen sie geeignet sind. Zu Demonstrationszwecken werden wir den berühmten Iris-Datensatz (Iris dataset) verwenden.
Also, R-Studio laden und loslegen!
install.packages("tidyverse")
library(datasets)
data("iris")
1. Balkendiagramme
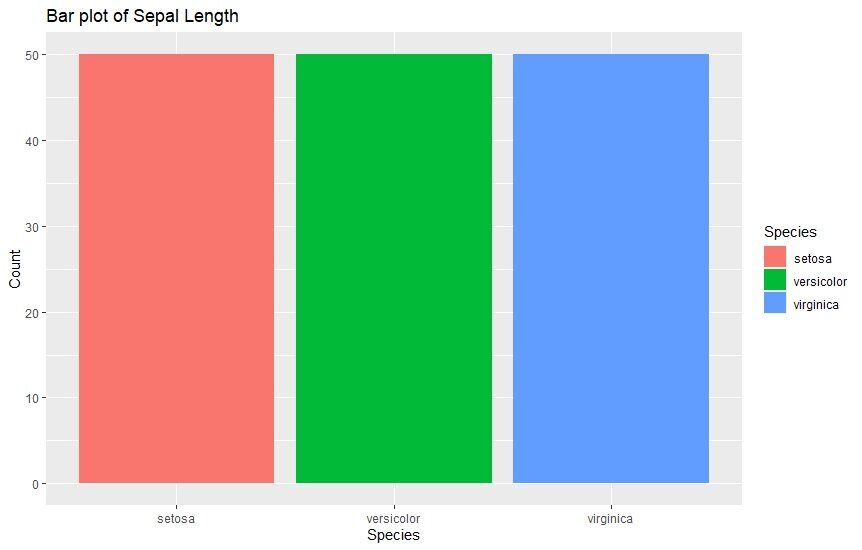
Balkendiagramme sind die gängigste Art von Diagrammen, die im Analytics verwendet werden. Sie eignen sich dazu um Werte verschiedener Kategorien mit Hilfe von vertikalen Balken zu vergleichen. Die unterschiedlich hohen Balken machen den Vergleich sehr einfach. Hier ist ein Beispiel, das die Sepal-Länge verschiedener Arten zeigt.
ggplot(data=iris, aes(x=Species, fill = Species)) +
geom_bar() +
xlab("Species") +
ylab("Count") +
ggtitle("Bar plot of Sepal Length")
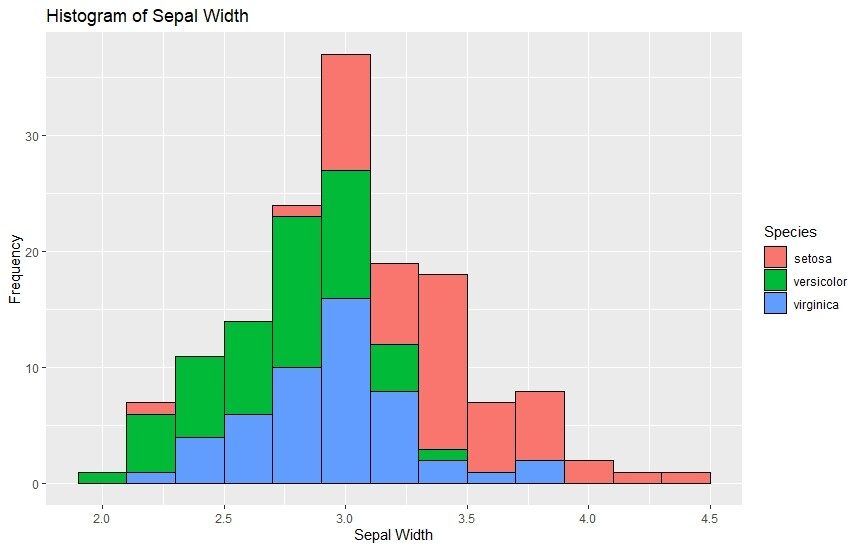
2. Histogramme
Histogramme sind den Balkendiagrammen sehr ähnlich. Sie werden verwendet, um fortlaufende Daten grafisch darzustellen und sie in bestimmte Bereiche zu gruppieren. Jeder Balken in einem Histogramm hat mehrere Bins mit unterschiedlichen Farben, welche die Häufigkeit jeder einzelnen Kategorie veranschaulichen. Unten sehen Sie ein Beispiel, wie Histogramme mit ggplot2 erstellt werden können.
ggplot(data=iris, aes(x=Sepal.Width)) +
geom_histogram(binwidth=0.2, color="black", aes(fill=Species)) +
xlab("Sepal Width") +
ylab("Frequency") +
ggtitle("Histogram of Sepal Width")
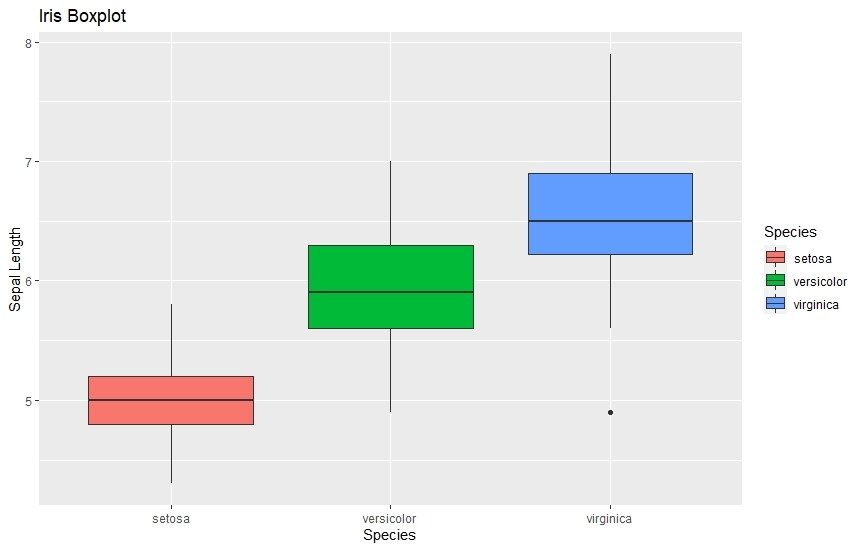
3. Box-Plot
Der Box-Plot stellt die gesamte Datenverteilung auf sehr kompakte Weise dar. Mit einer einzigen Box können Sie sowohl das obere und untere Quartil als auch etwaige Ausreißer sowie den Bereich der Datenverteilung anzeigen.
Möchten Sie wissen, wie man den Boxplot liest? Klicken Sie hier.
ggplot(data=iris, aes(x=Species, y=Sepal.Length)) +
geom_boxplot(aes(fill=Species)) +
ylab("Sepal Length") + ggtitle("Iris Boxplot")
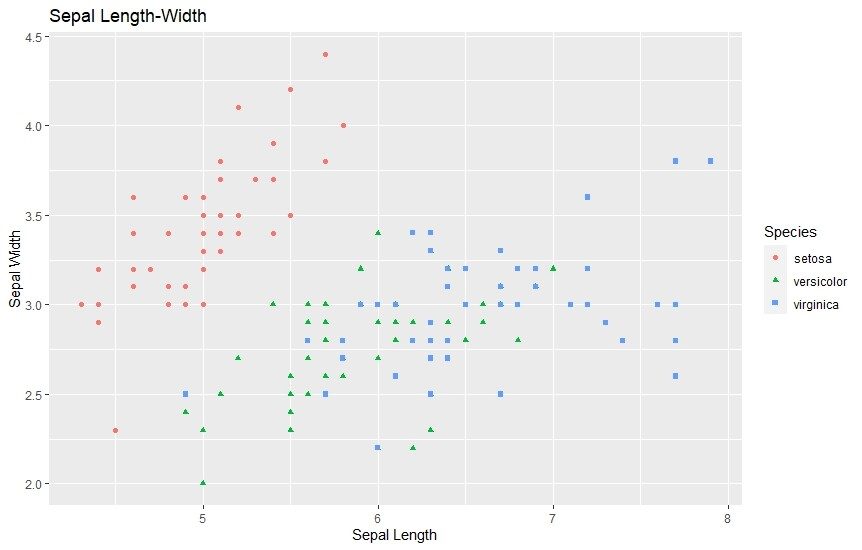
4. Streudiagramme
Nicht zuletzt sind auch Streudiagramme sehr verbreitet und eignen sich zur Darstellung von Daten. Sie werden häufig von Datenwissenschaftlern verwendet, um eine vorhandene Korrelation zwischen einer Reihe von Variablen zu erkennen. Es werden dabei alle Punkte einer Variablen in ein Diagramm gestreut. Gibt es eine Korrelation zwischen ihnen, so wird diese ersichtlich.
ggplot(data=iris, aes(x = Sepal.Length, y = Sepal.Width)) + geom_point(aes(color=Species, shape=Species)) +
xlab("Sepal Length") + ylab("Sepal Width") +
ggtitle("Sepal Length-Width")
Regressionsanalyse in R
Bei der Regressionsanalyse handelt es sich um ein statistisches Analyseverfahren, bei der die Beziehung zwischen den Variablen eines Datensatzes ermittelt wird. Häufig wird die Beziehung zwischen den unabhängigen und abhängigen Variablen ermittelt – ist aber kein Muss. Dies ist eine weitere wichtige Funktion zur Durchführung von Advanced Analytics mit R.
Die Idee der Regressionsanalyse ist es, herauszufinden, wie sich die Variable ändern wird, wenn wir eine andere Variable ändern. Genau auf diese Weise werden Regressionsmodelle erstellt. Es gibt verschiedene Arten von Regressionsverfahren, die wir je nach Form der Regressionslinie und Art der beteiligten Variablen verwenden können:
- Lineare Regression
- Logistische Regression
- Multinominale Logistische Regression
- Ordinale Logistische Regression
Schauen wir uns die verschiedenen Regressionsarten und ihre Verwendung genauer an.

1. Lineare Regression
Die lineare Regression ist die einfachste Art der Regression und kann verwendet werden, wenn zwei Variablen eine lineare Beziehung aufweisen. Ausgehend von den Werten der beiden Variablen wird eine gerade Linie mit der folgenden Gleichung formuliert:
Y = ax + b
Die lineare Regression wird zur Vorhersage fortlaufender Werte verwendet, wobei Sie lediglich den Wert der unabhängigen Variablen angeben. Als Ergebnis erhalten Sie den Wert der abhängigen Variable (in diesem Fall y).
2. Logistische Regression
Die logistische Regression wird angewandt, um die Vorhersage von Werten innerhalb eines bestimmten Bereichs zu ermitteln. Sie kann verwendet werden, wenn die Zielvariable kategorisch ist, z. B. zur Vorhersage eines Gewinners oder Verlierers anhand bestimmter Daten. Die folgende Gleichung wird bei der logistischen Regression verwendet.
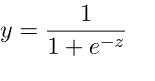
3. Multinomiale Logistische Regression
Wie der Name schon sagt, ist die multinomiale logistische Regression eine erweiterte Version der logistischen Regression. Der Unterschied zur einfachen logistischen Regression besteht darin, dass sie mehr als zwei kategoriale Variablen unterstützen kann. Ansonsten verwendet sie denselben Mechanismus wie die logistische Regression.
4. Ordinale Logistische Regression
Auch hier handelt es sich um einen erweiterten Mechanismus der einfachen logistischen Regression, der zur Vorhersage von Werten auf verschiedenen Kategorie Levels verwendet wird, z. B. zur Vorhersage von Rangfolgen. Ein Anwendungsbeispiel für die ordinale logistische Regression wäre die klassische Restaurantbewertung.
Verwendung von Regression in R
Zur Demonstration werde ich ein logistisches Regressionsmodell in R erstellen.
Anwendungsfall: Wir wollen den Erfolg von Schülern in einer Prüfung anhand ihrer IQ-Werte vorhersagen.
Lassen Sie uns dafür einige zufällige IQ-Zahlen generieren, um unseren Datensatz zu erstellen.
# Generate random IQ values with mean = 30 and sd =2
IQ <- rnorm(40, 30, 2)
# Sorting IQ level in ascending order
IQ <- sort(IQ)
Mithilfe von rnorm() haben wir eine Liste mit 40 IQ-Werten erstellt, die einen Mittelwert von 30 und einen STD von 2 haben.
Nun werden wir für 40 Schüler nach dem Zufallsprinzip Werte für bestanden/nicht bestanden als 0/1 erstellen und sie in einen Datenrahmen einfügen. Außerdem werden wir jeden von uns erstellten Wert mit einem IQ-Wert verknüpfen, damit unser Datenrahmen vollständig ist.
# Generate vector with pass and fail values of 40 students
result <- c(0, 0, 0, 1, 0, 0, 0, 0, 0, 1,
1, 0, 0, 0, 1, 1, 0, 0, 1, 0,
0, 0, 1, 0, 0, 1, 1, 0, 1, 1,
1, 1, 1, 0, 1, 1, 1, 1, 0, 1)
# Data Frame
df <- as.data.frame(cbind(IQ, result))
# Print data frame
print(df)
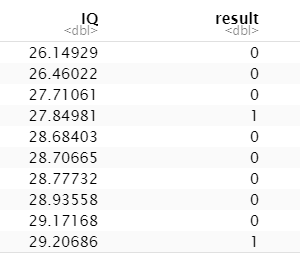
Lassen Sie uns nun ein Regressionsmodell auf der Grundlage unseres Datensatzes anlegen und eine Kurve erstellen, um zu sehen, wie das Regressionsmodell auf diesem Datensatz abschneidet. Wir können die Funktion glm() verwenden, um ein Regressionsmodell zu erstellen und zu trainieren, und die Funktion curve(), um die Kurve auf der Grundlage der Vorhersage zu zeichnen.
# Plotting IQ on x-axis and result on y-axis
plot(IQ, result, xlab = "IQ Level",
ylab = "Probability of Passing")
# Create a logistic model
g = glm(result~IQ, family=binomial, df)
# Create a curve based on prediction using the regression model
curve(predict(g, data.frame(IQ=x), type="resp"), add=TRUE)
# This Draws a set of points
# Based on fit to the regression model
points(IQ, fitted(g), pch=30)
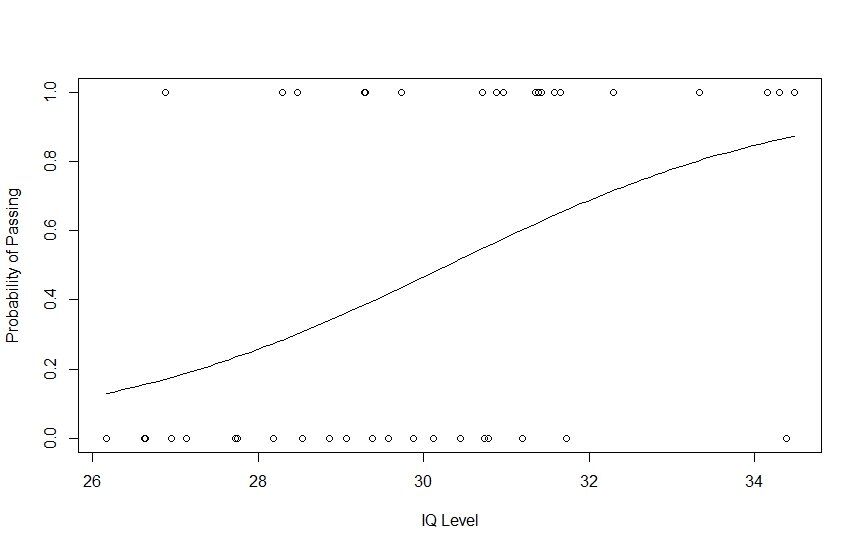
Wenn Sie die Statistiken des logistischen Regressionsmodells weiter überprüfen möchten, können Sie dies mit der Funktion summary() von R (summary(g)) ausführen.
Zeitreihenanalyse in R
Die Zeitreihenanalyse gehört zu den wichtigsten Stärken von R. Python ist zwar auch für die Zeitreihenanalyse bekannt, aber viele Experten sind der Meinung, dass R insgesamt eine bessere Anwendungsumgebung bietet. Das Zeitreihenanalyse-Paket ist sehr umfassend und das Beste, was man sich für Advanced Analytics mit R wünschen kann.
In diesem Artikel werden wir die folgenden Methoden der Zeitreihenanalyse behandeln:
- Naive Methode
- Exponentielle Glättung
- BATS and TBATS
Wir werden den in R vorhandenen Datensatz „Air Passengers“ verwenden, um Modelle für einen Validierungssatz und Prognosen für die Dauer des Validierungssatzes zu erstellen und schließlich den Mittleren Absoluten Prozentualen Fehler (Mean Absolute Percentage Error) ermitteln, um das Segment abzuschließen.
Initialisieren wir also die Daten zusammen mit dem Trainings- und Validierungsfenster, um zu beginnen.
# Time Series Forecast In R
install.packages("forecast")
install.packages("MLmetrics")
library(forecast)
library(MLmetrics)
data=AirPassengers
#Create samples
training=window(data, start = c(1949,1), end = c(1955,12))
validation=window(data, start = c(1956,1))
1. Naive Methode
Wie der Name schon sagt, ist die naive Methode die einfachste aller Prognosemethoden. Sie basiert auf dem einfachen Prinzip „was wir heute beobachten, wird morgen die Prognose sein“. Die saisonale naive Methode ist eine etwas komplexere Variante, bei der der Beobachtungszeitraum dem Zeithorizont entspricht, mit dem wir arbeiten, z. B. Woche/Monat/Jahr.
Lassen Sie uns mit einer saisonalen naiven Prognose fortfahren.
naive = snaive(training, h=length(validation))
MAPE(naive$mean, validation) * 100
Hier sehen wir einen MAPE-Wert von 27,05 %. Lassen Sie uns nun dieses Ergebnis grafisch darstellen.
MAPE-Wert = Mean Absolute Percentage Error
plot(data, col="blue", xlab="Year", ylab="Passengers", main="Seasonal Naive Forecast", type='l')
lines(naive$mean, col="red", lwd=2)
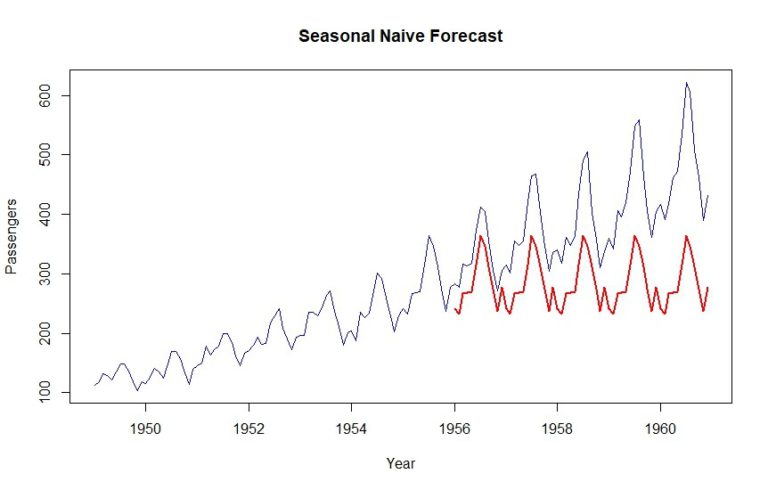
Wie Sie sehen können, wird der Datensatz des letzten Jahres für den Validierungszeitraum einfach wiederholt. Kurzgesagt, das ist eine saisonale naive Prognose.
2. Exponentielle Glättung
Die exponentielle Glättung bedeutet im Wesentlichen, dass die Beobachtungen weniger stark gewichtet werden. Wie bei gleitenden Durchschnitten erhalten die neuesten Beobachtungen ein höheres Gewicht, während die älteren allmählich an Gewicht verlieren.
Das Gute am Forecast-Paket ist, dass wir die optimalen exponentiellen Glättungsmodelle finden können, indem wir die Glättungsmethoden in die Struktur der Raummodelle einfügen.
ets_model = ets(training, allow.multiplicative.trend = TRUE)
summary(ets_model)
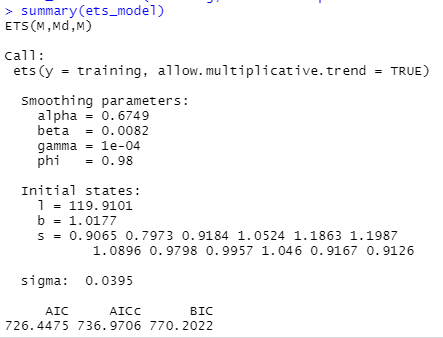
Nun werden wir das geschätzte optimale Glättungsmodell auf unsere ETS-Prognose anwenden und sehen, wie es abschneidet.
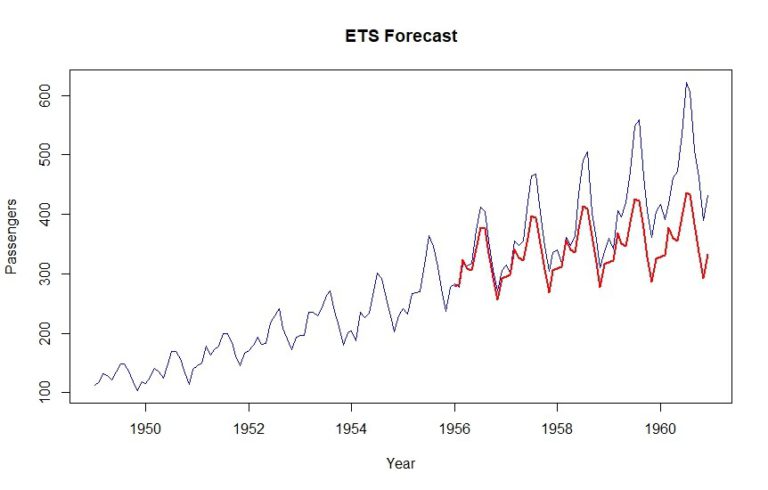
ets_forecast = forecast(ets_model, h=length(validation))
MAPE(ets_forecast$mean, validation) *100
Als Ergebnis erhalten wir einen MAPE von 12,6 %. Es ist offensichtlich, dass der Aufwärtstrend ein wenig gezählt wird.
3. BATS and TBATS
Für Prozesse, die sehr komplexe Trends aufweisen, ist ETS oft nicht aussagekräftig genug. Manchmal gibt es sowohl eine wöchentliche als auch eine jährliche Saisonalität. In diesem Fall zeichnen sich BATS und TBATS aus, da sie mehrere Saisonalitäten gleichzeitig verarbeiten können.
Erstellen wir ein TBATS-Modell und machen wir eine Vorhersage.
tbats_model = tbats(training)
tbats_forecast = forecast(tbats_model, h=length(validation))
MAPE(tbats_forecast$mean, validation) * 100
plot(data, col="blue", xlab="Year", ylab="Passengers", main="ETS Forecast", type='l')
lines(tbats_forecast$mean, col="red", lwd=2)
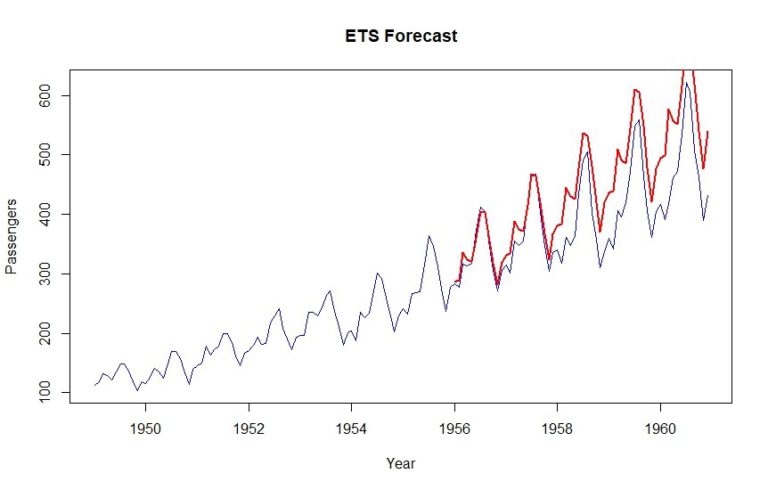
Wie Sie sehen können, wird mit dieser Methode ein MAPE von 12,9 % erreicht.
FAZIT
Ich habe in diesem Blog einen Überblick über die Advanced Analytics in R gegeben. Neben den Darstellungsmöglichkeiten und verschiedenen Arten der Regressionsanalyse wurde auch die Zeitreihenanalyse in R behandelt. Zeitreihen sind jedoch ein ziemlich umfangreiches Thema und wir haben bisher nur an der Oberfläche gekratzt. Im nächsten Blog Beitrag werden wir uns deshalb intensiv damit zu beschäftigen.
Bis dahin, viel Spaß mit R!
Dieser Blog ist Teil einer Serie von Beiträgen zur Business Analytics. Ich empfehle eine Business -Analytics-Platform aufzubauen. Ziel ist es, den Anwendern eine Plattform für Ihre Bedürfnisse zu bieten, wo sie alle Daten und Analytics-Tool finden.
Bisher veröffentlicht:
- Teil 1: Wie Business Analytics erfolgreich gestalten?
- Teil 2: Business Analytics vs. Business Intelligence
- Teil 3: Was ist SAP Analytics? Das SAP Data Warehouse-Portfolio
- Teil 4: SAP Analytics – Die Front End Produkte
- Teil 5: Data Plattform – Ein wichtiger Pfeiler der digitalen Transformation
- Teil 6: Auf dem Weg in die AWS
- Teil 7: Cloud – Fluch oder Segen?
- Teil 8: Mit Daten führen – warum Power BI häufig zur Auswahl steht
- Teil 9: Business Analytics Plattform: Agilität und Data Governance
- Teil 10: Advanced Analytics mit SAP und R
- Teil 11: Mit SAP PowerDesigner datenmodellgestützt entwickeln
- Teil 12: IBCS konforme Charts mit Tableau und graphomate
- Teil 13: Schnell neue Insights gewinnen: Ist jetzt der richtige Zeitpunkt, um mit der SAP Data Warehouse Cloud zu starten?
- Teil 14: Erste Schritte mit R