Iako je programski jezik R prisutan od ranih 90-ih, dobio je veliku slavu i pozornost u prethodnom desetljeću, uglavnom zbog svog širokog raspona funkcionalnosti povezanih sa statističkom analizom i znanošću o podacima. Značajan razlog je taj što ne zahtijeva čvrstu programsku pozadinu da bi ga ljudi počeli koristiti.
Nastavljajući našu seriju analitike s R, danas ćemo istražiti naprednu analitiku s R. Uključene su teme kao što su regresijska analiza s R-om i predviđanje vremenskih serija. Ako želite pogledati prethodni članak na temelju početničke razine analytics, slobodno kliknite ovdje.
Dakle, krenimo bez daljnjeg.
Iscrtavanje dijagrama programskim jezikom R
Počevši od osnova, pogledajmo sve različite vrste dijagrama koje možemo napraviti u R. Iako je crtanje grafova relativno jednostavan posao i moglo bi se reći da ne ispunjava uvjete za naprednu analitiku, bitno je poznavati različite vrste dostupnih dijagrama i kad koji koristiti ovisno o scenariju. Rezultati koje mogu pružiti u nekoliko redaka koda ponekad su značajniji od same napredne analitike. ggplot2 – Vaš najbolji prijatelj! Bez obzira kakve planove želite napraviti u R-u, ggplot2 bi uvijek trebao biti vaš prvi izbor. To je daleko najčešće korišteni paket od strane R-programera kada nešto planiraju. Pogledajmo različite parcele koje nudi paket ggplot2 i vidimo za koje su aplikacije prikladne. Za potrebe demonstracije koristit ćemo poznati skup podataka Iris. Dakle, pokrenimo RStudio i krenimo s planiranjem!
install.packages("tidyverse")
library(datasets)
data("iris")
1. Stupčasti dijagrami
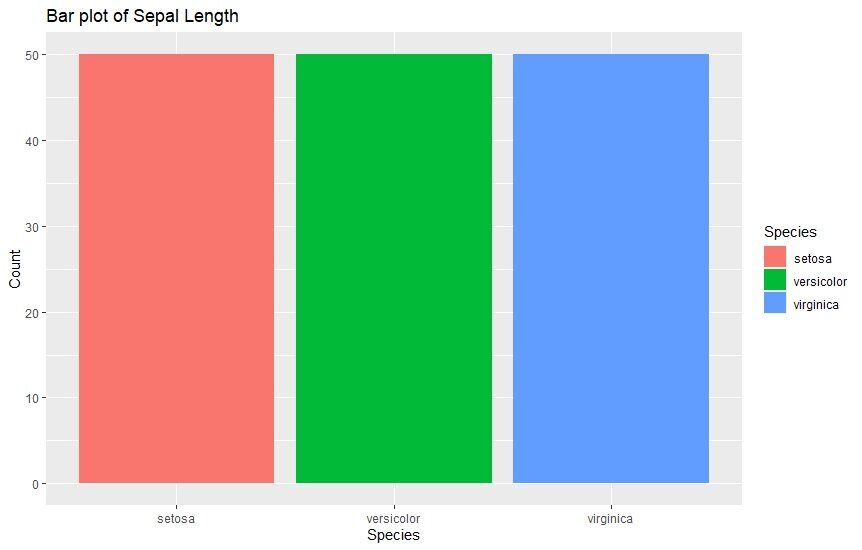
Stupčasti dijagrami su najčešća vrsta grafova koji se koriste u analizi. Koriste se kad god želite usporediti vrijednosti različitih kategorija pomoću okomitih traka koje predstavljaju vrijednosti. Ove šipke različite visine čine usporedbu vrlo prikladnom. Evo primjera koji prikazuje duljinu lapova različitih vrsta.
ggplot(data=iris, aes(x=Species, fill = Species)) +
geom_bar() +
xlab("Species") +
ylab("Count") +
ggtitle("Bar plot of Sepal Length")
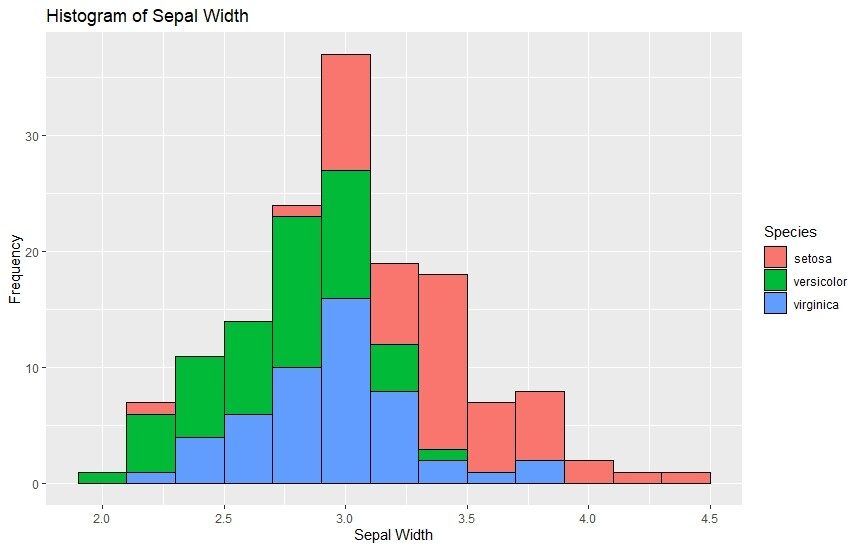
2. Histogrami
Histogrami su vrlo slični stupčastim dijagramima. Koriste se za grafički prikaz kontinuiranih podataka i grupiranje u spremnike. Svaka traka u histogramu ima više spremnika s različitim bojama što olakšava uvid u frekvenciju svake pojedinačne kategorije. Evo kako ih možemo napraviti pomoću ggplot2.
ggplot(data=iris, aes(x=Sepal.Width)) +
geom_histogram(binwidth=0.2, color="black", aes(fill=Species)) +
xlab("Sepal Width") +
ylab("Frequency") +
ggtitle("Histogram of Sepal Width")
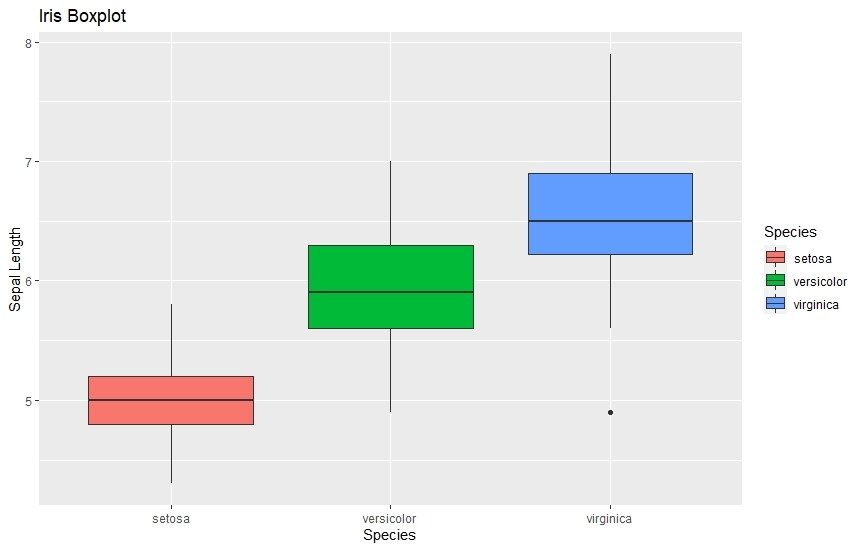
3. Box Plots
Box plot vizualizira cjelokupnu distribuciju podataka na vrlo kompaktan način. S jednim okvirom možete vidjeti i gornji i donji četvrt i sve prisutne vanjske vrijednosti, zajedno s rasponom širenja podataka. Zanima vas kako čitati box plot? Kliknite ovdje.
ggplot(data=iris, aes(x=Species, y=Sepal.Length)) +
geom_boxplot(aes(fill=Species)) +
ylab("Sepal Length") + ggtitle("Iris Boxplot")
4. Grafikon raspršenja
Posljednje, ali ne i najmanje važno, dijagrami raspršenja također su vrlo česti i koristan način pregledavanja podataka. Data scientists naširoko ih koriste kako bi vidjeli bilo kakvu postojeću korelaciju između skupa varijabli. Oni jednostavno raštrkaju sve točke varijable na dijagramu i ako postoji bilo kakva korelacija između njih, to postaje očito.
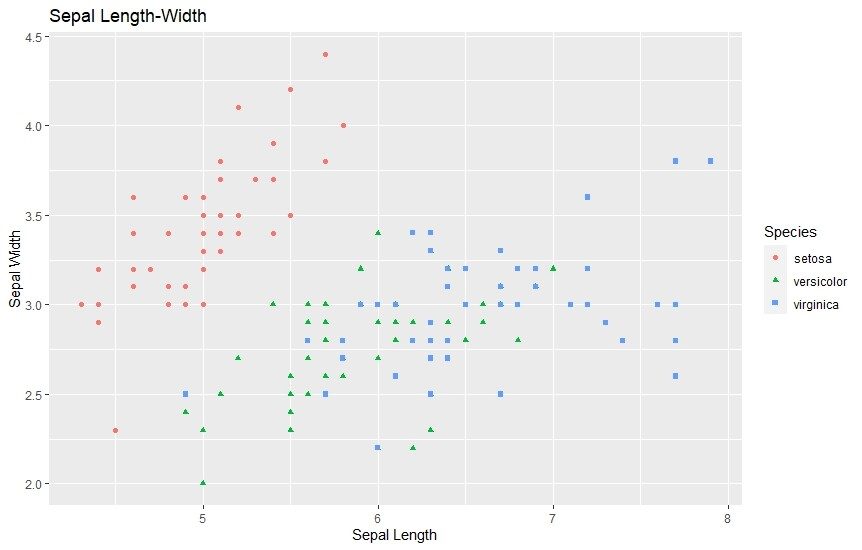
ggplot(data=iris, aes(x = Sepal.Length, y = Sepal.Width)) + geom_point(aes(color=Species, shape=Species)) +
xlab("Sepal Length") + ylab("Sepal Width") +
ggtitle("Sepal Length-Width")
Regresijska analiza u R
Regresijska analiza odnosi se na statističku obradu gdje se identificira odnos između varijabli u skupu podataka. Uglavnom utvrđujemo odnos između nezavisnih i zavisnih varijabli, ali to ne mora uvijek biti slučaj. Ovo je još jedna važna funkcija za naprednu analitiku s R. Ideja regresijske analize je pomoći nam da znamo kako će se druga varijabla promijeniti ako promijenimo jednu varijablu. Upravo tako se grade regresijski modeli. Postoje različite vrste regresijskih tehnika koje možemo koristiti na temelju oblika regresijske linije i vrsta uključenih varijabli:- Linearna regresija
- Logistička regresija
- Multinomijalna logistička regresija
- Redovna logistička regresija

1. Linearna regresija
Ovo je najosnovniji tip regresije i može se koristiti kada dvije varijable imaju linearni odnos. Na temelju vrijednosti dviju varijabli, ravna linija se modelira sljedećom jednadžbom: Y = ax + b Linearna regresija se koristi za predviđanje kontinuiranih vrijednosti gdje samo dajete vrijednost nezavisne varijable. Kao rezultat dobivate vrijednost zavisne varijable (y u ovom slučaju).2. Logistička regresija
Logistička regresija je sljedeća tehnika regresije koja se koristi za predviđanje vrijednosti unutar određenog raspona. Može se koristiti kada je ciljna varijabla kategorična, na primjer, predviđanje pobjednika ili gubitnika pomoću nekih podataka. Sljedeća se jednadžba koristi u logističkoj regresiji.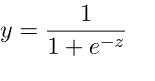
3. Multinomijalna logistička regresija
Kao što ime sugerira, multinomijalna logistička regresija je napredna verzija logističke regresije. Razlika između ove i jednostavne logističke regresije je u tome što može podržati više od dvije kategoričke varijable. Osim toga, koristi isti mehanizam kao logistička regresija.4. Ordinalna logistička regresija
Ovo je također napredni mehanizam za jednostavnu logističku regresiju, a koristi se za predviđanje vrijednosti koje postoje na različitim razinama kategorija, na primjer, predviđanje rangova. Primjer primjene upotrebe ordinalne logističke regresije bio bi ocjenjivanje vašeg iskustva u restoranu.Korištenje regresije u R
Sada, da vidimo kako možemo napraviti regresijsku analizu u R. Za demonstraciju, stvorio bih logistički regresijski model u R-u budući da lijepo pokriva koncepte. Slučaj upotrebe: Predvidjet ćemo uspjeh učenika na ispitu koristeći njihove razine kvocijenta inteligencije. Generirajmo neke nasumične IQ brojeve kako bismo došli do našeg skupa podataka.
# Generate random IQ values with mean = 30 and sd =2
IQ <- rnorm(40, 30, 2)
# Sorting IQ level in ascending order
IQ <- sort(IQ)
Koristeći rnorm(), napravili smo popis od 40 IQ vrijednosti koje imaju srednju vrijednost 30 i STD 2.
Sada smo nasumično kreirali vrijednosti za prolaz/neuspjeh kao 0/1 za 40 učenika i stavili ih u dataframe. Također, pridružit ćemo svaku vrijednost koju stvorimo s IQ-om kako bi naš podatkovni okvir bio potpun.
# Generate vector with pass and fail values of 40 students
result <- c(0, 0, 0, 1, 0, 0, 0, 0, 0, 1,
1, 0, 0, 0, 1, 1, 0, 0, 1, 0,
0, 0, 1, 0, 0, 1, 1, 0, 1, 1,
1, 1, 1, 0, 1, 1, 1, 1, 0, 1)
# Data Frame
df <- as.data.frame(cbind(IQ, result))
# Print data frame
print(df)
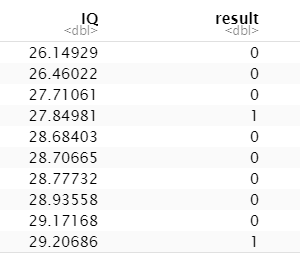
Sada napravimo regresijski model na temelju našeg skupa podataka i napravimo krivulju da vidimo kako se regresijski model ponaša na njemu. Možemo koristiti funkciju glm() za stvaranje i treniranje modela regresije i metodu curve() za crtanje krivulje na temelju predviđanja.
# Plotting IQ on x-axis and result on y-axis
plot(IQ, result, xlab = "IQ Level",
ylab = "Probability of Passing")
# Create a logistic model
g = glm(result~IQ, family=binomial, df)
# Create a curve based on prediction using the regression model
curve(predict(g, data.frame(IQ=x), type="resp"), add=TRUE)
# This Draws a set of points
# Based on fit to the regression model
points(IQ, fitted(g), pch=30)
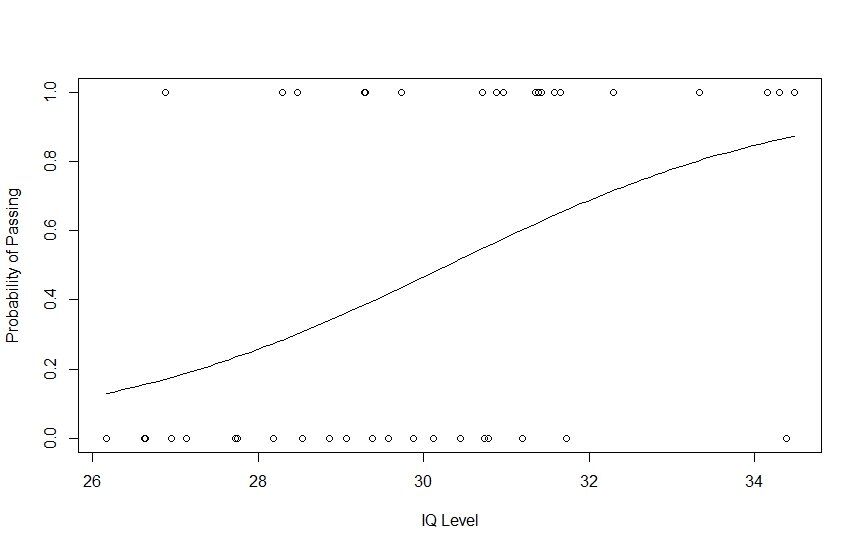
Štoviše, ako želite dodatno provjeriti statistiku modela logističke regresije, to možete učiniti pokretanjem summary() od R (summary(g)).
Predviđanje vremenskih serija u R
Predviđanje vremenskih serija među najjačim je odijelima R-a. Iako je Python također prilično poznat po analizi vremenskih serija, mnogi stručnjaci još uvijek tvrde da vam R pruža sveukupno bolje iskustvo. Paket prognoze je vrlo opsežan, a najbolje što se može poželjeti za naprednu analitiku s R. U ovom članku ćemo pokriti sljedeće metode predviđanja vremenskih serija:- Naivne metode
- Eksponencijalno zaglađivanje
- BATS i TBATS
# Time Series Forecast In R
install.packages("forecast")
install.packages("MLmetrics")
library(forecast)
library(MLmetrics)
data=AirPassengers
#Create samples
training=window(data, start = c(1949,1), end = c(1955,12))
validation=window(data, start = c(1956,1))
1. Naivne metode
Kao što naziv govori, naivna metoda je najjednostavnija od svih metoda predviđanja. Temelji se na jednostavnom principu “ono što danas promatramo, to će biti predviđanje za sutra”. Sezonska naivna metoda je malo složenija varijanta gdje se uzima period s kojim se radi, npr. tjedan/mjesec/godina. Idemo dalje sa sezonskom naivnom prognozom.
naive = snaive(training, h=length(validation))
MAPE(naive$mean, validation) * 100
Ovdje možemo vidjeti MAPE rezultat od 27,05%. Idemo naprijed i zacrtajmo ovaj rezultat.
MAPE rezultat = srednja apsolutna postotna pogreška
plot(data, col="blue", xlab="Year", ylab="Passengers", main="Seasonal Naive Forecast", type='l')
lines(naive$mean, col="red", lwd=2)
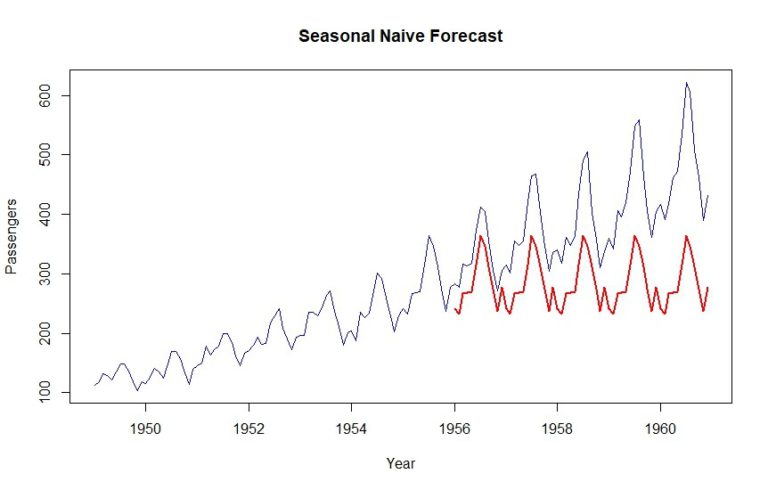
Kao što možete vidjeti, prošlogodišnji skup podataka jednostavno se ponavlja za validacijski period. To je ukratko sezonska naivna prognoza za vas.
2. Eksponencijalno zaglađivanje
Eksponencijalno zaglađivanje, u svojoj biti, odnosi se na smanjivanje težina opažanjima. Poput pomičnih prosjeka, najnovija opažanja dobivaju veću težinu, dok starija postupno smanjuju svoju težinu, otuda i važnost. Dobra stvar kod paketa za predviđanje je da možemo pronaći optimalne eksponencijalne modele izravnavanja stavljanjem metoda zaglađivanja unutar strukture prostornih modela.
ets_model = ets(training, allow.multiplicative.trend = TRUE)
summary(ets_model)
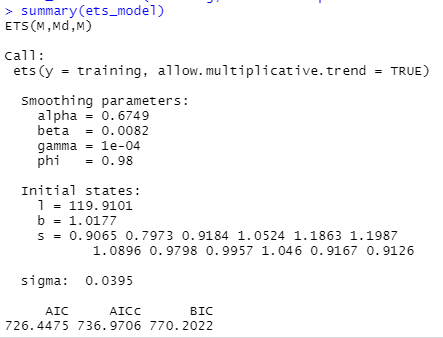
Sada ćemo uključiti procijenjeni model optimalnog zaglađivanje u našu ETS prognozu i vidjeti kakav će biti učinak.
ets_forecast = forecast(ets_model, h=length(validation))
MAPE(ets_forecast$mean, validation) *100
Kao rezultat, dobivamo MAPE od 12,6%. Također, vidljivo je da se uzlazni trend malo računa.
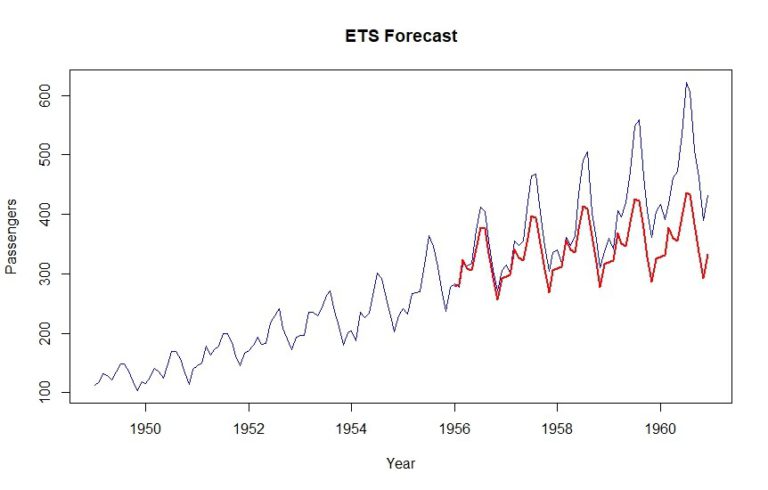
3. BATS i TBATS
Za procese koji imaju vrlo složene trendove, ETS često nije dovoljno dobar. Ponekad možete imati i tjednu i godišnju sezonalnost, a tu se ističu BATS i TBATS jer se mogu nositi s više sezonalnosti odjednom. Izgradimo TBATS model i napravimo predviđanje.
tbats_model = tbats(training)
tbats_forecast = forecast(tbats_model, h=length(validation))
MAPE(tbats_forecast$mean, validation) * 100
plot(data, col="blue", xlab="Year", ylab="Passengers", main="ETS Forecast", type='l')
lines(tbats_forecast$mean, col="red", lwd=2)
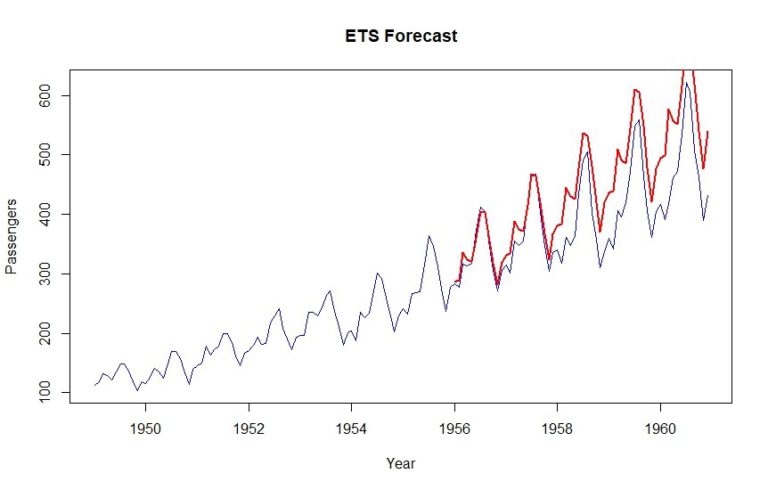
Kao što možete vidjeti, MAPE od 12,9% postiže se ovom metodom.
Zaključak
To je sve za danas! Naučili smo o naprednoj analitici u R-u koja se usredotočuje na crtanje i različite vrste regresijske analitike te smo dalje obrađivali prognozu vremenskih serija u R. Međutim, vremenske serije su prilično opsežna tema sama po sebi i još smo samo zagrebali površinu. Stoga ostanite s nama jer ćemo Time Series detaljno obrađivati u nadolazećim blogovima.
Do tada, sretan R-ing dečki!
